Measurement in Physics
In physics, a measurement is the result of an observation that can be expressed concisely as a number. Measurements are typically made in SI units, but many other measurement systems exist. For example, the size of objects such as planets and stars can be measured by observing the angle between their apparent positions in the sky and their position along a line of sight. The distance to a star or planet can be calculated by observing its parallax. Such measurements can be made with instruments on Earth, most commonly bolometers, photometers and spectrometers.
The SI System
The International System of Units (SI) is the modern form of the metric system and is likely the most familiar system of units to you. It works based on the fundamental unit for each physical quantity, with smaller derived units according to a set pattern. The SI defines seven base units from which all other SI units can be derived: length, mass, time, electric current, thermodynamic temperature, amount of substance and luminous intensity.
1. The Meter (m): This is the unit of distance. It is the distance travelled by light in a vacuum in a time of 1/299792459 seconds.
2. The kilogram (kg). This is the unit of mass. It is the mass of a certain quantity of a platinum-iridium alloy kept at the Bureau International des Poids et Mesures in France.
3. The second (s). This is the unit of time. A second is the duration of 9192631770 full oscillations of the electromagnetic radiation emitted in a transition between the two hyperfine energy levels in the ground state of a caesium-133 atom.
4. The ampere (A). This is the unit of electric current. It is defined as that current which, when flowing in two parallel conductors 1m apart, produces a force of 2 x 10^7 N on a length of 1 m of the conductors.
5. The kelvin (K). This is the unit of temperature. It is 1/273.16 of the thermodynamic temperature of the triple point of water.
6. The mole (mol). One mole of a substance contains as many particles as there are atoms in 12g of carbon-12. This special number of particles is called Avogadros number and is approximately 6.02 x 10^23.
7. The candela (cd). This is a unit of luminous intensity. It is the intensity of a source of frequency 5.40 x 10^14 Hz emitting 1/683 W per steradian.
Significant Figures
When a number is not expressed using scientific notation, it is said to be expressed in "decimals". The number of significant figures of a quantity in science is the number of digits known with certainty. For example, the mass of an object can be known precisely if it has been weighed to an accuracy greater than or equal to 1mg; however, if it has been weighed to an accuracy less than 1mg but greater than or equal to 0.1mg then only 2 significant figures can be known for certain.
Rules for Finding Significant Figures
1. Writing a number in scientific notation involves writing it as axe 10b, where b is either a positive or negative integer and a is a decimal where 1 <= a <= 10. The number of significant figures in an is given by the number of digits in that number.
2. The outcome of any operation involving multiplication, division, raising a number to a power, or taking a root must have the same number of significant figures as the input number.
3. The least number of decimal places in the numbers being added or subtracted must match the number of decimal digits in the result when adding and subtracting.
4. When writing values to the appropriate number of decimal places or significant figures, follow the rules for rounding.
Uncertainties and Errors
The final number used in an experiment is known as the "result". It is only when an experiment is actually carried out that this "result" becomes the true value of the quantity being measured. In order to determine whether or not a measurement has been accurate, one must first measure the uncertainty associated with it. The units with which these uncertainties are measured will matter, depending on which quantity you wish to measure.
Types of Uncertainty
1. Systematic Errors: These are situations where a number is measured without adequate precision to ensure the accuracy of the final measurement.
2. Random Errors: These include errors that are caused by unpredictable and uncontrollable sources such as human error, contamination, interference and equipment malfunction.
Question: Do errors need to be added or subtracted? If yes, then what rules must be followed?
Answer: Definitely the total error would be sum of individual errors. To find out more about errors and operations performed on them kindly visithttps://youtube.com/channel/UCoqI7C9rI2UbFPITF2bPgnQ
Accuracy and Precision
If a measurements systematic error is minimal, it is said to be accurate in physics. Consequently, the measured value is practically extremely close to the accepted value for that amount (assuming that this is known - it is not always). If the random uncertainty is low, a measurement is said to be precise. This indicates that the individual values were quite close to one another in practice when the measurement was performed numerous times.
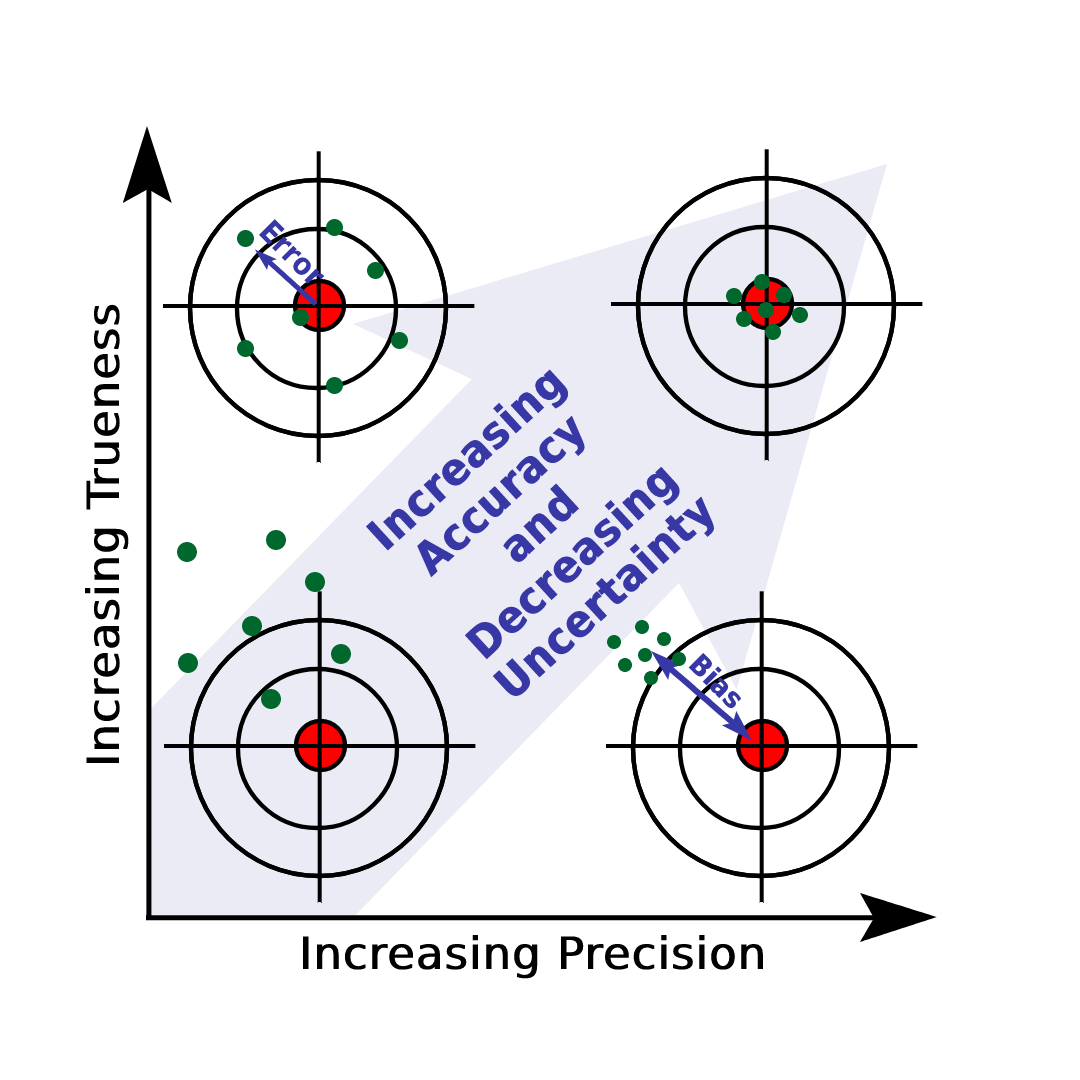
Question: Show with the help of examples the difference between accuracy and precision.
Answer: We know that accurate value is different from precise value, but to clearly understand this you can visit the channelhttps://youtube.com/channel/UCoqI7C9rI2UbFPITF2bPgnQ.

Vectors And Scalars
In physics, some quantities, such as time, space, mass, speed, and temperature, can be expressed by a single number. We refer to these as scalar quantities. For instance, it suffices to state that the temperature is -5.0°C or that a body weighs 64 kg. However, many quantities are only fully stated when a direction is required in addition to a number. We dont know where youll be in 30 minutes if you say youre leaving Paris right now in a 220 km/h train since we dont know which way youre going to travel. Quantities that require both a direction and a magnitude are referred to as vector quantities.
